前段时间做结构光三维重建的时候用到了格雷码编码方法，这里正好做一下总结。
这里讨论的是典型的二进制格雷码（Binary Gray Code），简称格雷码，由贝尔电话实验室研究物理学家Frank Gray提出。Frank Gray 1969年过世，这里所提的Gray码是他在1940年研究出来的，用来在PCM（Puslue Code Modulation）方法传送信号时避免错误。1953年3月17日，Gray取得美国专利，这是格雷码第一次出版的日期。
在一组数的编码中，若任意两个相信的代码只有一位二进制数不同，则称这种编码为格雷码，另外由于最大数与最小数之间也仅一位数不同，即“首尾相连”，因此又称循环码或反射码。前面提到格雷码的提出是为了避免讯号传送错误，原理是什么呢？很简单，在数字系统中，常要求代码按一定顺序变化。比如数字3（二进制011）切换到相信的数字4（二进制100），装置的三个位元都要转换，但是在实际电路中，3位变换不可能绝对同时发生，则计数中可能出现短暂的其它代码，可能导致电路状态错误。格雷码可以避免这种错误。
1
2
3
4
5
6
7
8
| 十进制 格雷码 二进制
0 000 000
1 001 001
2 011 010
3 010 011
4 110 100
5 111 101
6 101 110
|
下面谈一下一个喜闻乐见的问题：格雷码生成。
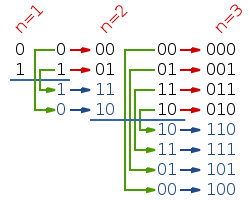
格雷码有一种天然的递归算法：如果要求n位的格雷码，那就先n-1位的；假设G(n-1)表示所有n-1位的格雷码，于是n位格雷码可以用下面的两步构造出来，第一步，把G(n-1)中各个元素左边都加一个0.第二步，把G(n-1)中各个元素的顺序反过来排列，并且在前面都加一个1.由此得到的合集就是格雷码G(n)。
1
2
3
4
5
| G(1)={0,1}
G(2)=0{0,1}∪1{1,0}={00,01,11,10}
G(3)={000,001,011,010,110,111,101,100}
G(4)={0000,0001,0011,0010,0110,0111,0101,0100,
1100,1101,1111,1110,1010,1011,1001,1000}
|
证明也很简单，数学归纳法。当n=1时，{0，1}。如果比n-1小或等于的格雷码都可以用那两条规则构造出来。对于G(n)的前半部分，把0去除显然满足格雷码的性质，加上0同样满足；后半部分亦然。接口部分差异在于第一位的0和1，即只相差1位。G(n)的元素个数为G(n-1)的两倍，即2的n次方，完备性。证毕。简单用C++实现如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| vector<string> generateGraycode(int n)
{
vector<string> ans;
if(n==1)
{
ans.push_back("0");
ans.push_back("1");
}
else
{
vector<string> mid_ans = generateGraycode(n-1);
for(vector<string>::iterator iter=mid_ans.begin(); iter!=mid_ans.end(); ++iter)
{
string temp = *iter;
temp.insert(0, "0");
ans.push_back(temp);
}
for(int i=mid_ans.size()-1; i>=0; --i)
{
string temp = mid_ans[i];
temp.insert(0, "1");
ans.push_back(temp);
}
}
return ans;
}
|
另一种方法直接生成。稍微仔细观察一下不难发现，最后一位交替改变（0变1,1变0），在每两步改变之间，改变最右边的1的左边的位元（0变1，1变0）。比如G(4)，0000，先改变最后一位0，得到0001，然后改变最右边1的左边的位元得0011；然后再次改变最后一位得0010，直到1000.简单实现~
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| void gray(int n)
{
int i;
char code[MAXN];
for(i=0; i<n; i++)
code[i] = '0';
code[n] = '\0';
printf("%s\n", code);
while(1)
{
if(code[n-1]=='0')
code[n-1] = '1';
else
code[n-1] = '0';
printf("%s\n", code);
i = n-1;
while(code[i]=='0') i--;
if(i==0)
break;
if(code[i-1]=='0')
code[i-1]='1';
else
code[i-1]='0';
printf("%s\n", code);
}
}
|
等等，写到这里还没有结束。还记得汉诺塔问题吗？一定要记得啊，因为我不想再复述了:D。
那么汉诺塔问题与格雷码有什么关系呢？我们知道汉诺塔问题要求一次移动一个圆盘，对应到格雷码，如果我们把最小的圆盘对应为格雷码的最后一位，我们会发现格雷码的改变位元正好对应相应的圆盘。还有个问题，就是第1块圆盘的移动有两种选择。不过不要紧，再稍加观察一下，我们就会发现第1块圆盘的移动是有规律的。假设圆盘最开始所在的柱子编号为1，最终都要移动到编号为2的柱子上，另外一个柱子编号为3。我们发现当盘子总数为奇数时，第1块圆盘的移动序列为123123…；总数为偶数时，移动序列为132132…。至于其它圆盘的移动，稍加判断就可以了。那么一个解汉诺塔问题的非递归算法就出来。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
| void gray_hanoi(int n)
{
stack<int> *peg = new stack<int>[3];
vector<int> order;
order.push_back(1);
for(int i=n; i>0; i--)
peg[0].push(i);
char code[N];
for(int i=0; i<n; i++)
code[i] = '0';
code[n] = '\0';
if(n%2)
{
order.push_back(2);
order.push_back(3);
}
else{
order.push_back(3);
order.push_back(2);
}
int times = 0;
while(1)
{
if(code[n-1]=='0')
code[n-1] = '1';
else
code[n-1] = '0';
cout << "Move 1 from peg" << order[times%3] << " to peg" << order[(times+1)%3] << endl;
peg[order[times%3]-1].pop();
peg[order[(times+1)%3]-1].push(1);
times++;
int pos = n-1;
while(code[pos]=='0') pos--;
if(pos==0)
break;
pos--;
if(code[pos]=='0')
code[pos]='1';
else
code[pos]='0';
int from, to;
for(int i=0; i<3; i++)
{
if(!peg[i].empty() && peg[i].top()==n-pos)
from = i;
else if(peg[i].empty() || peg[i].top()>n-pos)
to = i;
}
peg[from].pop();
peg[to].push(n-pos);
cout << "Move " << n-pos << " from peg" << from+1 << " to peg" << to+1 << endl;
}
}
|
下面是当圆盘总数为4个时候的运行结果
无聊的同学可以手动验证一下:)
其实还有一个类似很有趣的问题：九连环问题。篇幅有限，这里就先不写了。大家回去自己看看吧！另外在集合的分割问题中，格雷码也有应用，等下次有空再写吧！
Happy New Year! Happy Weekend!
参考：《C语言名题精选百则》
wiki: 格雷码、汉诺塔、九连环, etc