聊一聊哈希表

0. 引言

hash table，中文可以称作哈希表。简单来说就是提供 (key, value) 的存取，当然只存 key 也是可以的。一般来说哈希表的插入和查找的平均时间复杂度都为 O(1)，因此在日常工作中使用也较为广泛。

1. General Hash Table

1.1 实现

为了保证插入和查找的平均复杂度为 O(1)，hash table 底层一般都是使用数组来实现。对于给定的 key，一般先进行 hash 操作，然后相对哈希表的长度取模，将 key 映射到指定的地方。

1	index = hash(key) % hash_table_size // index 就是 key 存储位置的索引

这里的核心在于如何选取合适的 hash 函数，如果提前知道 key 的一些相关信息，往往可以选取一个不错的 hash 函数。常用的 hash 函数有 SHA-1，SHA-256，SHA-512，这里就不再赘述了。

1.2 冲突处理

冲突，也叫做碰撞，意思是两个或者多个 key 映射到了哈希表的同一个位置。冲突处理一般有两种方法：开放定址（open addressing）和开链（separate chaining）。

开放定址的意思是当发生冲突时，我们从当前位置向后按某种策略遍历哈希表。当发现可用的空间的时候，则插入元素。开放地址有一次探测、二次探测和双重哈希。一次探测是指我们的遍历策略是一个线性函数，比如依次遍历冲突位置之后的第 1，2，3…N 位置。如果直接遍历 1，4（=2^2），9 (=3^2)，这就是二次探测的一个例子。双重哈希就是遍历策略间隔由另一个哈希函数来确定。

下图是开放地址解决冲突问题的一个例子。key “John Smith” 和 “Sandra Dee” 在 index = 152 位置出现冲突，使用开放地址的方法将 “Sandra Dee” 存放在 index = 153 的位置。之后 key “Ted Baker” 的映射位置为 index = 153，又出现冲突，则将其存放在 index = 154 的位置。由这个例子我们可以看出这种处理方法的一个缺点：解决旧问题的同时会引入新的问题。

开链的思想是哈希表中的每个元素都是一个类似链表或者其他数据结构的 head。当出现冲突时，我们就在链表后面添加元素。这也就意味着，如果某一个位置冲突过多的话，插入的时间复杂段将退化为 O(N)。补充一点，如果哈希表的每个元素都是一个链表头的，那么又可以分为头存储元素和不存储元素两种，如下图所示。

简单比较一下这两种处理方法的优劣：开放定址在解决当前冲突的情况下同时可能会导致新的冲突，而开链不会有这种问题。同时开链相比于开放定址局部性较差，在程序运行过程中可能引起操作系统的缺页中断，从而导致系统颠簸。

1.3 Rehash

很多语言或者工具包哈希表的内部实现都使用了两个数组，其中一个作为备用。如果当前哈希表的负载因子（元素个数/哈希表容量大小）过大或者过小时，就需要将数据切换到备用数组里面，这个过程就是 rehash。新的哈希表的大小可以有很多种方案，比如 redis 里面的哈希表（字典的底层实现）扩展时，新的哈希表的大小为大于当前哈希表里面存放元素的 2 倍的最小的 2 的 n 次幂。

Rehash 过程也很有讲究，这个过程不应该影响当前系统的运行，所以比较推崇的一种方法是渐进式 rehash。渐进式 rehash 的主要思想是在 rehash 阶段对于新的写请求，并不会写入老的哈希表里面，而是直接写入到新的哈希表里；对于读请求，优先读取新的哈希表，如果不存在，则去读老的的哈希表同时将这条数据迁移到新的哈希表里面来。

Rehash 有一个问题需要讨论一下：如何鉴定 rehash 阶段的开始与结束？开始很简单，每次写操作或者定期检测一下负载因子，当满足条件则开始 rehash。那么如何鉴定结束呢？一种比较常规的方法是定期检测，但是这涉及到很多问题，比如如何界定检测的时间粒度。另一种是记录下迁移过程。还是以 Redis 为例来说明，Redis 使用的是 1.2 介绍的哈希表元素作为链表头不存储元素的方式，这样数据迁移的时候只需要从原链表将节点删除，然后插入到新的哈希表对应的位置就好了。同时哈希表结构有一个字段记录了老的哈希表残留的数据，这样我们只需要检测这个变量（代价很小）就知道 rehash 有没有完成了。rehash 过程如下图所示（来自《Redis 设计与实现》）

迁移索引 1 和 2 上的过程图略去。

2. Bloom Filter

哈希表的问题在于空间利用率不够高。对于某些我们需要排重场景（存储的只有一个 key，不是<key,value>），比如写爬虫的时候我们需要做网址排重，这个时候使用 Bloom Filter（中文又称作布隆过滤器）就比较高效。

Bloom filter 的主要思想是使用位图+多个哈希函数。省空间的常用方法就是使用位图；单个哈希函数容易导致冲突，所以采用多个哈希函数。具体方法是预先分配一个大数组用作位图，对于每个 key 的写入，使用多个哈希函数映射到位图上的不同位置。对于 key 的查找，位图上的所有映射位置都为 1 时才表示 key 存在。用伪代码描述如下。

var bitmap
func insert(key) {
    for h := range hashs {
        bitmap.setone(h(key))
    }
}

func lookup(key) bool {
    for h := range hashs {
        if bitmap.get(h(key)) != 1 {
            return false
        }
    }
    return true
}

下面看一个具体的例子，如下图。插入 x, y, z 分别将多个 hash 函数计算出来的位置 bit 置为 1。这时候集合包含了三个元素 {x, y, z}，此时要查找 w，通过 hash 函数计算出来的位置如下图所示，由于有一个 bit 不是 1，所以可以确定 w 不再集合里面。

上面只说到了插入和查找，那么删除呢？bloom filter 是不支持删除的。除此之后 bloom filter 对于不存在的 key 的查找是存在误判率的，但是这个概率对于大部分使用场景来说都是可接受的。关于误判率的具体推算可以参考其他资料，比如 wikipedia，这里就不细说了。

这里是我实现的一个简单的 bloom filter：https://github.com/legendtkl/bloomfilter

3. Cuckoo Filter

Bloom Filter 的最大缺点在于不支持删除操作。如果要实现删除操作的话则需要进行计数，这样就不满足空间效率高这一条初衷了。一种替代方案是使用 Cuckoo Filter，当然前提是也是可以容忍一定的误判率的。

3.1 简介

Cuckoo 是布谷鸟的意思，也就是我们常说的杜鹃。“鸠占鹊巢”里面的“鸠”的就是类似杜鹃这种鸟类。而 Cuckoo Hash 的就是采自“鸠占鹊巢”的意思。和普通的哈希表不同，在 Cuckoo Hash 表中，每个元素在 bucket list 中有两个位置可以存放。如果两个位置都被其他元素占了，则随机选择一个位置将其踢走。被踢走的元素被移动到它的备用位置，如果也被其他元素占了则也将其踢走，如此反复。下图是 Cuckoo Hash 的示例。

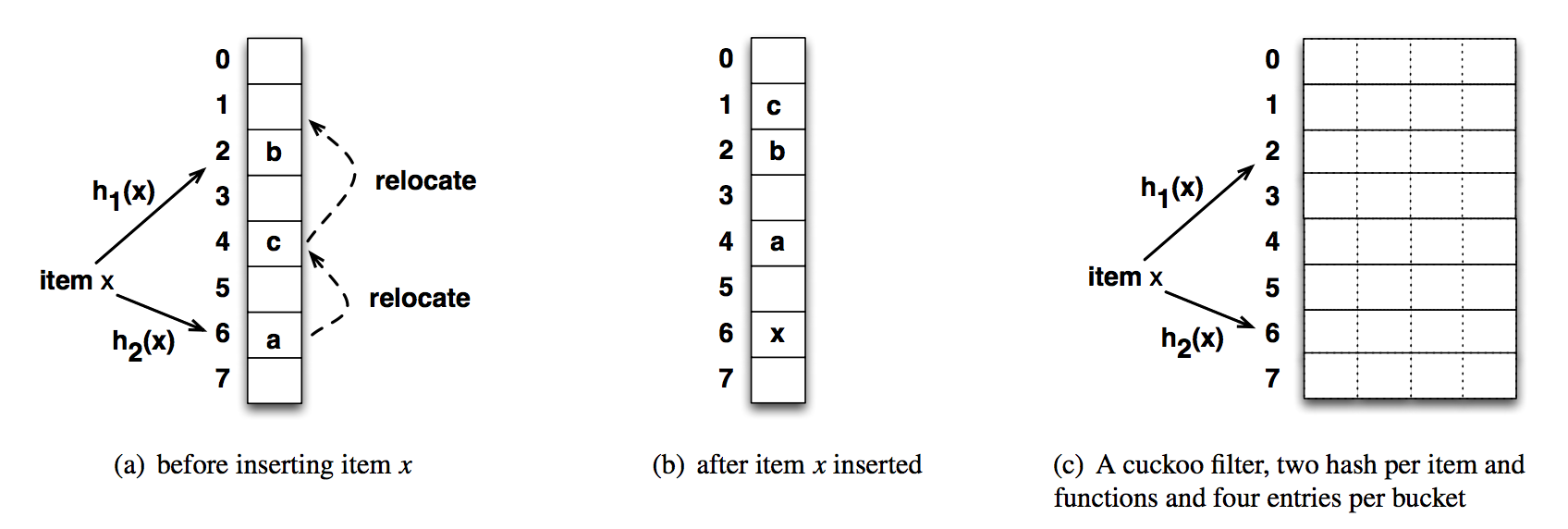
如上图所示，(a) 表示插入元素 x 之前已经存在的元素 a, b, c。通过计算 x 的两个可用位置分别被 a, b 占用了，随机选择一个位置，也就是元素 a 存放的位置。然后元素 a 被迁移到它的备用位置，也就是元素 c 现在的位置。类似的 c 再做迁移。(c) 表示 Cuckoo Hash 的一种实现，每个 bucket 有四个 slot。对于 (a) 的情形，则直接把 x 插入到元素 a 或 b 所在的 bucket 的空的 slot 里面即可。

Cuckoo Filter 是 Cuckoo Hash 的一种更节省空间的变体，它在 bucket 中存放的不是元素本书，而是 fingerprint(x) 值，也是类似于一种哈希值。

3.2 插入 x

假设对于 x 的两个可用位置为 i1, i2。当出现 x 需要迁移的时候，我们怎么得到它的另一个位置呢？因为 bucket 里面存放的是 f = fingerprint 值，所以 i1，i2 不能简单的通过两个哈希函数计算得到。这里使用异或运算达到 i1，i2 可以互相转化的目的。具体算法如下。

另外在我们为元素再分配地址（下面简称 reallocate）的时候，如果一直找不到空闲的位置（比如 x, y 的两个可用位置 i1, i2 完全相同），或者可以找到但是需要的时间出于性能方面的考虑不能忍受，这个时候就需要我们做一个限制，比如设置一个最大的 reallocate 的次数。

f = fingerprint(x);
i1 = hash(x)
i2 = i1 xor hash(f)
if bucket[i1] or bucket[i2] has an empty entry then
    add f to that bucket;
    return Done
// relocate existing items
i = randomly pick i1 or i2
for n = 0; n < MaxNumKicks; n++ do
    randomly select an entry e from bucket[i]
    swap f and the fingerprint stored in entry e;
    i = i xor hash(f)
    if bucket[i] has an empty entry then
        add f to bucket[i]
        return Done
return Failure

3.3 查找 x

查找很简单，但是需要注意的是存在误判的。

f = fingerprint(x)
i1 = hash(x)
i2 = i1 xor hash(f)
if bucket[i1] or bucket[i2] has f then
    return True
return False

3.4 删除

删除也是删除的元素 fingerprint 值，存在误删的情况。

f = fingerprint(x)
i1 = hash(x)
i2 = i1 xor hash(f)
if bucket[i1] or bucket[i2] has f then
    remove a copy of f from this bucket
    return True
return False

3.5 关于 fingerprint

前面说到 Cuckoo Filter 是存储了元素 x 的 fingerprint(x) 值从而达到节省空间的目标的。那么这里就有一个问题肯定会有多个元素计算得到的 fingerprint 值相同，其实问题不大，以为元素还有一个备用位置，两个备用位置都相同的概率就比较小了。那么如果我们插入相同的元素呢？在我们实现的时候每个 bucket 可以有多个 slot，那么我们最多则可以插入 2 * slot.size() 个相同的元素。

关于 Cuckoo Filter 的性能冲突等的讨论可以查看附录里面的论文: cuckoo filter: practically better than bloom。关于 Cuckoo Filter 的实现可以看 Coolshell 上面的那篇文章 Cuckoo Filter：设计与实现。

4. 总结

哈希表由于其性能较好，在日常工作中经常使用到，各个语言也都实现了这种数据结构。关于哈希表其实还有很多可以讨论的，比如分布式哈希表（DHT），但是限于篇幅有限，这里就不再赘述了。

5. 参考

Hash Table – wikipedia
《Redis 设计与实现》
Bloom Filter – wikipedia
cuckoo hash – wikipedia
cuckoo filter: practically better than bloom
Introduction to Distributed Hash Table