打算写一个三维重建(3D Reconstruction)的专题,不是介绍理论,而是如何动手写一个三维重建系统。那么什么是三维重建呢?简单来说,就是将物体的三维的位置,也就是三维坐标,重建出来,当然说到位置那么当然是相对于某一坐标系的。三维重建方法有很多种,我打算写的是基于双目的重建。打个比方,人的双眼就是一个双目系统,我们能准确地判断一个物体距离我们有多远就是因为双目的原因。三维重建主要包括三个关键模块:摄像机标定、图像对应点确定、三角重建。这次主要介绍摄像机标定。
在讨论摄像机标定之前,理应讨论一个摄像机成像模型以及公式推导。我们先看摄像机模型中最简单的针孔模型,高中的物理课堂上大家应该都学过,错了,是初中。如下图。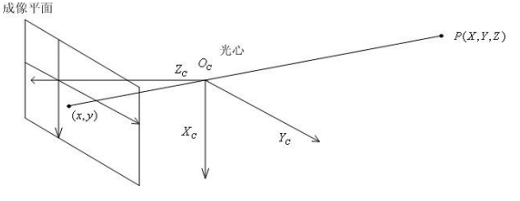
则有下面公式成立。
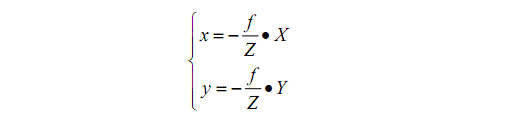
上式中f为摄像机成像平面与光心的距离,也就是成像焦距。上述成像模型即为光学中的中心投影模型,也称为针孔模型。针孔模型主要由光心投影中心、成像面与光轴组成。模型假设物体表面的部分反射光经过一个针孔而投影到像平面上,也就是成像过程满足光的直线传播条件,为一个身影变换过程。由于成像平面位于耀原点的后面,因此称为后投影模型,此时像点与特点为的坐标符号相反;为简便起见,在不改变像点与物点的大小比例关系的前提下,可以交成像平面从光心后前移至光心前,此时空间点坐标与像坐标之间的符号相同,成等比例缩小的关系,此种模型称为前投影模型。下面就使用前投影模型来讨论。
还没结束呢,在实际使用摄像机的过程中,人们为了方便计算,常常设置多个坐标系,因此,空间点的成像过程必然涉及到坐标系之间的相互转化,包括旋转与平移。旋转可以分解成绕三个轴的旋转。平移就是一个平移向量。这部分比较简单,就不说了。这里内容有点多,感觉这里说的不是很清楚,之后再补充吧。大家可以参考《计算机视觉:一种现代方法》。
对摄像机成像模型了解了之后,我们可以得到世界坐标系中的三维点到图片坐标系的二维坐标的变换公式如下。
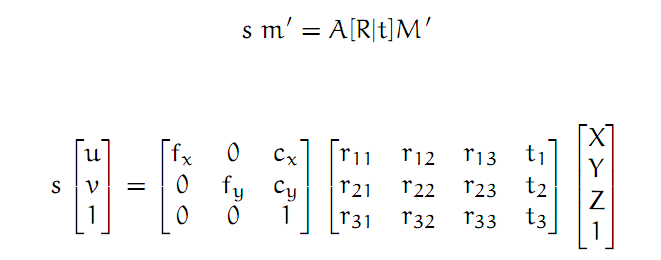
其中(u,v,1)是图像坐标系中的点的齐次坐标,(X,Y,Z,1)为世界坐标系中的点的齐次坐标。简单说一下,图像坐标系就是我们用摄像机拍摄出来的图像上的坐标系,单位是像素。坐标原点为像素(0,0)的点,x轴为横坐标,y轴为纵坐标。三维坐标系采用右手系,当然也可以自己定义左手系,这些顶多只会影响点的绝对坐标,并不会影响相对关系。世界坐标系就是点的真实坐标所有的坐标系。一般后面我们用棋盘格来标定的话,世界坐标系就是建立在棋盘格上的,这个后面在说。上面公式中A是摄像机的内参数,包括像素焦距fx,fy,和中心点像素坐标,注意这些都已经从长度单位换算成像素单位了。后面的R和T就是图像坐标系与世界坐标系的旋转矩阵与平衡矩阵了。这是不考虑畸变系数。有时候我们要考虑畸变,包括径向畸变和切向畸变。考虑了畸变,相当于对上面得到的(u,v)再进行一次畸变校正,可以用下图表示。
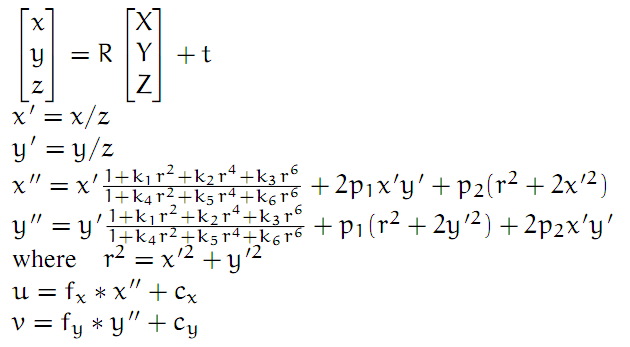
上面公式中的k1,k2,k3,k4,k5,k6就是径向畸变,一般只取得k3,因为后面的影响已经很小了。p1和p2是切向畸变。所谓摄像机定标就是求这样参数。下次再写吧。
周二晚上,锤子手机发布会,我从头看完了,虽然没有让人特别眼前一亮的创新,但是150项微创新也是够诱人的。如果我们足够仔细,会发现QQ也是这么走过来的。以前人们经常说,享受过程,但是在这个浮躁的社会,更多的人看问题都是结果导向的。事做成了牛逼,没做成呵呵。“在你没有做出成绩之前,这个世界才不会在意你的尊严!”