这次要介绍的Tsai提出的基于RAC的定标方法是计算机视觉相机标定方面的一项重要工作,该方法的核心是利用径向一致约束来求解除(相机光轴方向的平移)外的其它相机外参数,然后再求解相机的其它参数。基于RAC方法的最大好处是它所使用的大部分方程是线性方程,从而降低了参数求解的复杂性,因此其定标过程快捷,准确。
相机模型前面已经说过了,这里就不说了,下面要说的是径向一致约束和定标算法。先回顾一下世界坐标系和相机坐标系的关系: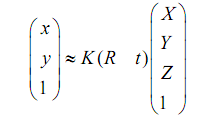
K的话为相机内参:
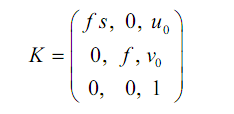 ]
]
理想图像坐标到数字图像坐标的变换(只考虑径向偏差),如下图
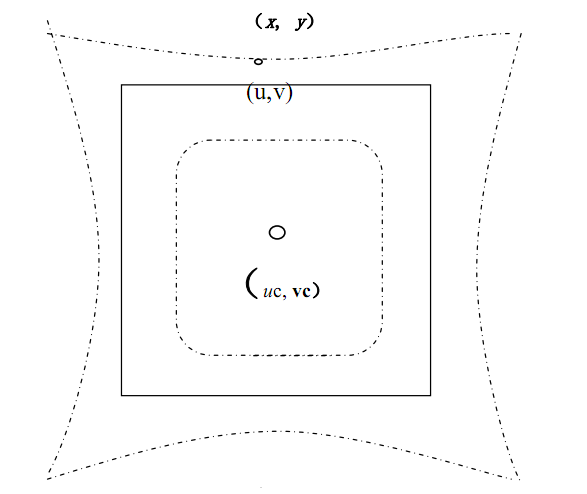
对于径向畸变满足下式,径向畸变系数只取了一阶,后面的k2,k3不考虑。
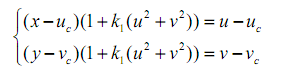
式中(u,v)为一个点在图像坐标系中的坐标,(x,y)为畸变校正后的坐标,(uc,vc)为畸变中心
1.径向一致约束。图像平面上,点(uc,vc),(u,v),(x,y)共线,则有
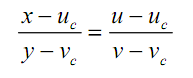
通常把图像中心取作畸变中心和主点的坐标,因此有下式
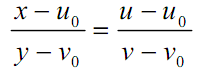
2.定标算法
定标步骤一:求解相机外参数旋转矩阵R和x,y方向上的平移向量t1,t2。根据前面世界坐标系与相机坐标系的关系,将R和t展开,可以求得
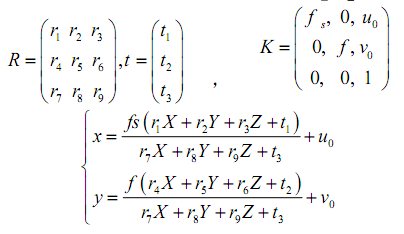
再由上面的径向一致约束得到
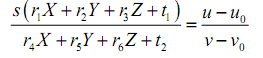
由至少7组对应点,可以求得一组解:M0=(m1,m2,m3,m4,m5,m6,m7,m8)≈(sr1,sr2,sr3,st1,r4,r5,r6,t2),对M0除以c=sqrt(m5^2+m6^2+m7^2),则得到一组解(sr1,sr2,sr3,st1,r4,r5,r6,t2)。由r1^2+r2^2+r3^2=1可以求出S,从而t1也可以求出来
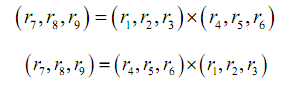
定标步骤二:求有效焦距f, z方向上的平移t3和畸变系数k
令k=0作为初始值,则由上面x,y的表达式有:

再由x,y的表达式,可以将第一步求出R,t1,t2的值代入得:
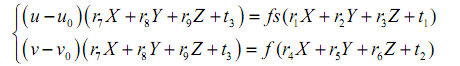
由此可以求得f,t3。将求出的f,t3以及k=0作为初始值,对下式进行线性优化,估算出t3,f和k的真实值。
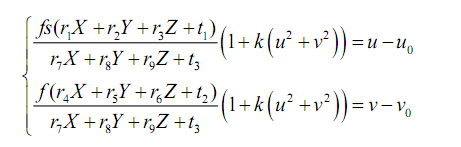
都是数学就不贴代码了,下次说说我们常用的棋盘格标定吧!